LAS LEYES DE NEWTON:
PRIMERA LEY O LEY DE LA INERCIA:
Todo cuerpo permanece en su estado de reposo o de movimiento rectilíneo uniforme al menos que una fuerza actúe sobre él.
Esta ley nos quiere decir, que si no hay ninguna fuerza externa, los cuerpos o no se mueven o permanecen en movimiento rectilíneo uniforme.
SEGUNDA LEY DE NEWTON O PRINCIPIO FUNDAMENTAL DE LA DINÁMICA:
La fuerza que actúa sobre un cuerpo es directamente proporcional a su aceleración en relación a su masa.
De esta ley extraemos la principal fórmula de la dinámica:
Donde m = masa y a = aceleración
La unidad de la fuerza es el Newton que se representa con la letra N. Un newton es igual a:
TERCERA LEY DE NEWTON O PRINCIPIO DE ACCIÓN – REACCIÓN:
Cuando un cuerpo ejerce una fuerza sobre otro, éste ejerce sobre el primero una fuerza igual y de sentido opuesto.
Cuando sucede esto, es cuando no hay movimiento. Para que haya movimiento, la fuerza ejercida tiene que superar a la que es ejercida por el objeto en sentido opuesto.
EJEMPLO DE EJERCICIOS SOBRE LAS LEYES DE NEWTON:
1. Se ejerce sobre un objeto de 3Kg de masa una fuerza que hace que el objeto adquiera una aceleración de 5m/s2. ¿Qué valor tiene la fuerza ejercida?
INTERACCIÓN ENTRE FUERZAS:
Sobre un mismo cuerpo actúan diferentes fuerzas, por tanto, realmente la fórmula de la fuerza es:
Las fuerzas que se ejercen sobre un mismo objeto toman distintas direcciones, ya que las fuerzas son vectores (porque tienen dirección y sentido). Cuando dos fuerzas tienen sentido opuesto debemos restarlas y cuando tienen el mismo sentido debemos sumarlas.
Además existen algunas fuerzas con nombre específico:
1. EL PESO:
El peso es la fuerza que ejerce la gravedad sobre un objeto:
Esta fuerza se describe por la siguiente fórmula:
Esta fuerza no infiere en el movimiento mientras el objeto se encuentre en una superficie plana, pero si lo hace cuando la superficie tiene pendiente.
2. LA FUERZA NORMAL:
La fuerza normal es la fuerza que ejerce la superficie sobre los objetos que se encuentran en ella:
La fuerza normal siempre es perpendicular al suelo, a la superficie donde se apoya el objeto.
En una superficie plana, esta fuerza se contrarresta con el peso, lo que hace que ambas no influyan en el movimiento. En una superficie inclinada, la fuerza normal se contrarresta con la componente y del peso, de la que hablaremos más tarde.
3. LA FUERZA DE ROZAMIENTO:
La fuerza de rozamiento es una fuerza que ejerce la superficie en contra del movimiento, y por lo tanto, es una fuerza que frena el movimiento. La fórmula de la fuerza de rozamiento es la siguiente:
Donde N es la fuerza normal y μ es el coeficiente de rozamiento. Debemos decir que existen dos coeficientes de rozamiento el coeficiente de rozamiento estático (μe) que es el que se da cuando el objeto no está en movimiento, y el coeficiente de rozamiento dinámico (μd) que es el que se da cuando el objeto se mueve.
En muchos ejercicios de física, se contempla la fuerza de rozamiento como nula, pero en otros no.
Por tanto lo que debemos hacer para obtener la fuerza final que intervienen en un objeto es fijarnos en las fuerzas que intervienen y en su dirección.
EJEMPLO DE EJERCICIOS DE INTERACCIÓN ENTRE FUERZAS:
1. Dos personas empujan una caja de 5Kg de masa que se encuentra en una superficie horizontal. La primera lo hace con una fuerza de 10N y la segunda con una fuerza de 12N, ambos en la misma dirección. La superficie tiene un coeficiente de rozamiento dinámico de 0,2. ¿Cuál es la aceleración que lleva el objeto?
En primer lugar debemos hacer siempre un esquema de las fuerzas que actúan sobre el objeto:
En segundo lugar debemos encontrar las fuerzas que no sabemos a través de sus fórmulas:
En primer lugar hayamos el peso:
Sabemos que:
Entonces:
Sabemos que en una superficie horizontal, el peso y la fuerza normal se anulan, por tanto, P = N, entonces, N = 49N.
Por último debemos encontrar la fuerza de rozamiento, que sigue la siguiente fórmula:
Entonces:
Una vez sabemos el valor de todas las fuerzas, para encontrar la aceleración debemos aplicar la fórmula general de la dinámica:
Por tanto:
Debemos indicar los signos en función de las direcciones de las fuerzas. Tomaremos como positivas la F1 y F2, porque estas son las que favorecen el movimiento, y la fuerza de rozamiento negativa, porque va en contra del movimiento. El peso y la normal, debemos colocarlo uno con cada signo porque se anulan entre sí, y no influyen en el movimiento.
Resolvamos entonces:
PLANOS INCLINADOS:
Cuando el objeto se encuentra en un plano inclinado en lugar de en una superficie horizontal, es necesario descomponer fuerzas. Las fuerzas que debemos descomponer son todas aquellas que se encuentren fuera de los ejes del plano inclinado. Veamos:
Dibujemos las fuerzas que actúan en este sistema. En primer lugar debemos dibujar el peso, que siempre es perpendicular a la tierra:
En segundo lugar dibujamos la fuerza normal, que siempre es una fuerza que ejerce el suelo, por lo que la dibujamos así:
Para poder trabajar con estas fuerzas debemos descomponer en un eje de coordenadas colocado a favor de la superficie inclinada donde trabajamos:
Las fuerzas que no se encuentren paralelas a los ejes, deberán ser descompuestas. Entonces, en este caso, debemos descomponer el peso:
Una vez descompuestas las fuerzas, debemos saber, que para poder solucionar los problemas necesitamos conocer trigonometría. En este caso vemos que:
EJEMPLO:
Un objeto se desplaza por una superficie inclinada hacia abajo sin que se aplique ninguna fuerza externa. Si la fuerza de rozamiento tiene un coeficiente de μ = 0,2, el plano inclinado un ángulo de 30º y el objeto una masa de 25 kg, ¿Qué aceleración llevará el objeto?
En primer lugar debemos hacer un esquema de las fuerzas y descomponer las que sea necesarias para poder solucionar el problema.
Si nos fijamos, veremos que la componente del peso del eje y, y la fuerza normal se contrarrestan. No pasa como en el plano inclinado, donde la normal es igual al peso simplemente.
Esto quiere decir que Py = N. Así solo actúan en el movimiento las fuerzas que tienen componente x.
Estas fuerzas serán Px, que es la que promueve el movimiento, y la fuerza de rozamiento, que se opone al movimiento. Así debemos encontrar en primer lugar el valor de FF:
Sabemos que:
Y en este caso, la fuerza normal es igual a Py, por tanto:
Sabemos que Py = P · sinα, entonces:
El peso es P = m · g, entonces:
Substituimos para encontrar la fuerza de rozamiento:
Ahora debemos encontrar el Peso de la componente x, que será Px = P · cosα, entonces:
Sabemos que el peso es P = m · g, entonces:
Substituimos y encontramos la fuerza Px:
Aplicamos la fórmula general de la dinámica:
En este caso:
Ambas fuerzas se restan porque tienen sentidos contrarios.
Sustituyendo por los valores encontraremos el valor de la aceleración:
FUERZAS CON ÁNGULO:
Hasta ahora hemos visto siempre ejemplos en que las fuerzas aplicadas tenían una dirección horizontal, pero, también podemos hablar de fuerzas que se aplican con algún ángulo, y deberemos trabajarlas de forma distinta.
Para trabajar con fuerzas que tienen un ángulo, también deberemos descomponerlas, es decir, utilizar la trigonometría.
En relación al movimiento, tendremos que ver, que sólo la componente x de las fuerzas implica el movimiento del objeto. La componente y es una fuerza vertical que no tiene implicación en el movimiento, sino que actúa junto con el peso y la fuerza normal, no teniendo ninguna implicación en el sistema, ya que en un plano horizontal, el peso y la fuerza normal tiene que ser igual a cero.
EJEMPLO:
Una persona estira un objeto de 20 kg con una fuerza de 20 N con un ángulo de 40º. Si contemplamos el rozamiento como nulo. ¿Qué aceleración llevará el objeto?
En primer lugar debemos hacer un gráfico con las fuerzas que intervienen en el sistema.
Ahora podemos ver, como la única fuerza que actúa en el movimiento es la componente x de la fuerza, porque el resto de fuerzas son verticales, así que no influyen en el movimiento.
Siguiendo las razones trigonométricas, vemos que:
Entonces, solucionamos la fuerza aplicando la fórmula:
Una vez sabemos el valor de Fx podemos aplicar la fórmula general de la dinámica para saber el valor de la aceleración:
En este caso solo tenemos una fuerza, así que:
Solucionamos aplicando la fórmula:
ESTÁTICA:
La estática, es el estudio de los objetos cuando no se encuentran en movimiento, es decir, cuando están en equilibrio.
Este tipo de ejercicios suelen tener que ver con deportes como la escalada, o con objetos en suspensión.
Es importante destacar, que cuando un objeto se encuentra en equilibrio, es decir, sin movimiento, la fórmula general de la dinámica es la siguiente:
EJEMPLO:
Un objeto de 2,5 Kg de masa, se encuentra suspendido en un sistema como el siguiente, donde hay con el techo un ángulo de 45º con cada una de las cuerdas:
Indica el valor de las tensiones que actúan en el sistema para que el objeto se encuentre en equilibrio.
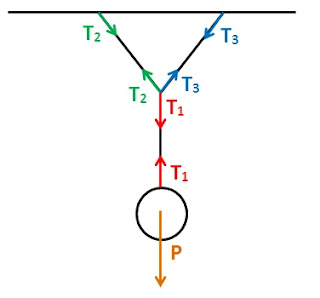
En primer lugar haremos un esquema con las fuerzas que actúan en este sistema:
La Tensión es una fuerza que se da cuando el objeto se encuentra sujeto por cuerdas. Es aquella fuerza que genera la fuerza en contra del objeto. Debemos dibujarla siempre en los dos lados de la cuerda, y saber que será la misma en un extremo y el otro de la cuerda.
Como este sistema tiene dos partes, debemos en primer lugar dividir el sistema en dos para encontrar las tensiones.
En primer lugar nos fijamos en la parte de la bola y la primera cuerda:
Si analizamos el sistema vemos que, para que el objeto se encuentre en equilibrio, el valor de la tensión 1 tiene que ser igual al peso del objeto, de lo contrario, el sistema se partiría, y la bola no podría sostenerse en la cuerda. Así buscamos el valor del peso:
El valor del peso es 24,5 N, entonces, el valor de T1 también es 24,5 N.
Una vez hemos solucionado esta parte del sistema, nos dirigimos a solucionar la otra parte del sistema:
En este caso, deberemos descomponer las Tensiones 2 y 3 ya que no se haya en el mismo eje de coordenadas que el resto de fuerzas del sistema:
En esta parte del problema, deberemos siempre separar las fuerzas que actúan en el eje x de las que actúan en el eje y.
Veamos que componentes actúan en el eje x:
Esto es:
Ahora veamos que componentes actúan en el eje y:
Esto es:
Como vemos, hemos generado dos ecuaciones con dos incógnitas, por tanto, para solucionar esto, debemos generar un sistema de ecuaciones:
Ahora solucionamos el sistema con cualquiera de los métodos para resolver sistemas de ecuaciones. Yo lo haré a través del método de Sustitución.
Ahora sabemos que T2 = T3, por lo tanto, que las dos tensiones en este caso son iguales. Esto sucede porque el ángulo es el mismo y porque además el seno y el coseno de 45º es el mismo.
Sustituimos en la otra ecuación, para obtener T3:
Como hemos obtenido que T3 y T2 son iguales, el valor de T2 también será 17,5 N.








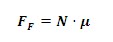
















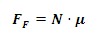

















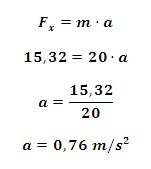













No hay comentarios:
Publicar un comentario