SISTEMAS DE ECUACIONES
Un sistema de ecuaciones es un grupo con diferentes
ecuaciones y diferentes incógnitas donde el resultado de esas incógnitas es
común a todas las ecuaciones.
Lo que debemos saber en primer lugar, es que para, resolver
un sistema de ecuaciones tiene que haber tantas incógnitas como ecuaciones. Hay
tres métodos para resolver ecuaciones, ahora vemos a continuación como podemos
resolver los sistemas a través de este sistema:
1. MÉTODO
DE IGUALACIÓN:
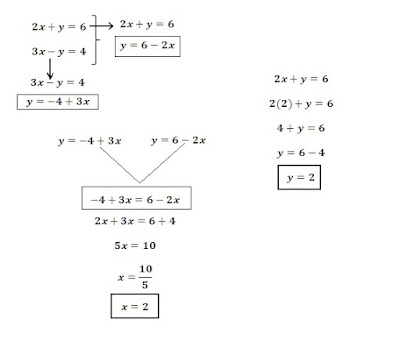
Con este método, en primer lugar aislamos una incógnita (la
misma) en las dos ecuaciones:
Una vez hemos aislado una de las incógnitas, las igualamos,
entonces:
Ahora resolvemos esta nueva ecuación, y así encontramos la
otra incógnita:
Una vez se ha encontrado una de las incógnitas, la otra la encontramos
colocando el valor de esta en una de las ecuaciones y encontramos la otra:
2. MÉTODO
DE SUSTITUCIÓN:
Con este método lo primero que hacemos es aislar una de las
incógnitas en una ecuación:
Lo siguiente que haremos será sustituir lo que hemos obtenido
al igualar en la otra ecuación:
Ahora solucionamos esta ecuación para obtener una de las
incógnitas:
Una vez obtenida esta incógnita, con la otra que hemos
aislado antes y sustituyendo la que ya conocemos encontramos la otra:
3. MÉTODO
DE REDUCCIÓN:
Con el método de reducción lo que haremos es restar las dos
ecuaciones, multiplicándolas o dividiéndolas para conseguir que una de las incógnitas
desaparezca.
En nuestro caso no debemos ni multiplicar ni dividir
ecuaciones porque una de las ecuaciones tiene ya una incógnita que se elimina,
porque se encuentra multiplicada por el mismo número y con signo contrario.
Así desempeñamos la suma de las dos ecuaciones:
Ahora para encontrar esa incógnita, acabamos de resolver la
ecuación:
Finalmente sustituimos la incógnita obtenida en cualquiera de
las dos ecuaciones primeras y encontramos la otra incógnita:
Lo que si debemos saber, es que independientemente del método
que usemos es necesario que siempre nos dé el mismo resultado.












No hay comentarios:
Publicar un comentario