CÁLCULO DE LÍMITES:
Para funciones normales (polinómicas, racionales,…) y la función está definida en un punto a, el
límite es el resultado de la función en ese punto.
Por ejemplo:
Tenemos que tener en cuenta que no podremos calcular los
límites, si no están dentro del dominio de una función. Así, no podremos
calcular el límite en números negativos de funciones con radicales.
Sin embargo, si podremos calcular los límites de funciones
racionales aunque busquemos el límite donde no hay dominio, porque en los
valores cercanos a este, si hay dominio.
CÁLCULO DE LOS LÍMITES
EN UNA FUNCIÓN DEFINIDA A TROZOS:
Cuando tenemos una función definida a trozos, deberemos
encontrar los límites en los puntos de unión de los diferentes trozos.
Calcularemos los límites laterales por la izquierda y por la derecha en función
de los trozos que determina cada lado.
Por ejemplo:
Vemos que la función viene determinada por los puntos -1 y 1.
Calcularemos los límites para cada uno de esos valores.
Para determinar el límite para x = -1 por la izquierda de función, se define con la primera parte
de la función. (Para indicar que buscamos
definir una función por la izquierda, añadiremos el signo (-) a la derecha del
límite):
Para determinar el límite para x = -1 por la derecha, se define con la segunda parte de la
función, tal como indican las condiciones. (Para
indicar que buscamos definir una función por la derecha, añadiremos el signo (+)
a la derecha del límite):
Ahora sabemos que para x
= -1, los límites son:
Como en los dos casos coincide el resultado, sabemos que para x
= -1 existe límite y vale 1.
Ahora determinaremos los límites de la misma forma para x = 1.
En primer lugar por la izquierda:
Finalmente por la derecha:
Así los límites para x =
1 son:
Como en este caso los límites no coinciden, para x = 1 no existe
límite.
LÍMITES EN EL INFINITO:
Cuando una función tiende a infinito, el resultado del límite
siempre será infinito o menos infinito. Esto lo podemos comprobar fácil,
considerando las x como (+) y ver si el resultado nos quedaría positivo o
negativo:
Vemos
que el resultado sería positivo, porque los números valores darán resultados
positivos, porque son positivos. Por tanto el resultado será positivo.
En
este caso, como los valores mayores son negativos, el resultado resultaría cada
vez más negativo, y por tanto el resultado será negativo.
Cuando queremos definir el límite de una función para menos
infinito, haremos lo mismo pero considerando las normas de los números enteros
para los números negativos, y determinaremos si el resultado será positivo o
negativo:
Si
analizamos vemos que al multiplicar, los negativos pasarían a ser positivos. Y
por tanto, el resultado será cada vez más positivo.
En
este caso, como el monomio, más grande acaba siendo multiplicado por un número
negativo, el resultado será negativo.
LÍMITE DE LA INVERSA DE
UN POLINOMIO:
El límite de la inversa de un polinomio será igual a 0:



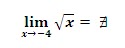












No hay comentarios:
Publicar un comentario