MOVIMIENTOS
CIRCULARES:
Son aquellos movimientos en que la
trayectoria es circular.
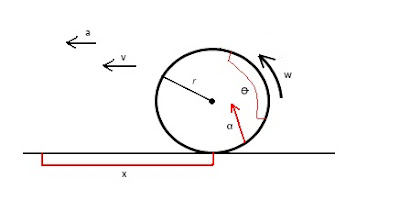
Los movimientos circulares tienen dos
componentes, uno circular y otro horizontal, ya que si imaginamos una rueda,
podemos contemplar como al igual que se produce un movimiento circular, este
genera otro movimiento horizontal que hace que se desplace el coche.
Componente
circular
|
Componente
horizontal
|
Ɵ
= Espacio circular recorrido
Expresamos en: rad
|
x
= Espacio lineal recorrido
Expresamos en: metros
|
w
= Velocidad angular
Expresamos en: rad/s
2π rad = 1 vuelta = 1 revolución
|
v=
Velocidad lineal
Expresamos en: m/s
|
α
= Aceleración angular
Expresamos en: rad/s2
|
a
= Aceleración lineal.
Expresamos en: m/s2
|
r
= Radio
|
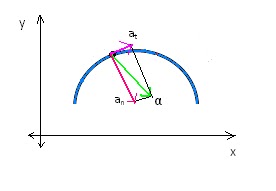
La aceleración angular tiene dos componentes:
Los dos componentes de la aceleración son perpendiculares, y así
tenemos la aceleración tangencial (at) y la aceleración normal (an).
La aceleración tangencial es la que se encarga de la variación de
la velocidad angular, por tanto, en movimientos uniformes, no encontraremos
aceleración tangencial nunca.
Aun así la fórmula de la aceleración tangencial es:
La aceleración normal, dirigida al interior del objeto circular,
se encarga de que el movimiento tenga trayectoria circular, por lo que esta
aceleración estará siempre presente en un movimiento circular.
La fórmula de la aceleración normal es:
EL PERIODO Y LA FRECUENCIA:
1. Periodo: Tiempo que se tarda en dar una vuelta completa.
2. Frecuencia: Cantidad de vueltas que se dan en 1 segundo. Se
mide en Hertz (Hz).
TIPOS DE MOVIMIENTOS CIRCULARES:
1.1) Movimiento Circular Uniforme (MCU):
El movimiento circular uniforme (MCU) es aquel que tiene una trayectoria circular, y que tiene velocidad angular (w) constante. Esto quiere decir que la aceleración angular es nula.
Ecuación del movimiento:
Ecuación del movimiento lineal:
Fórmula que relaciona la velocidad angular y lineal:
Gráfica del movimiento circular uniforme:
Ejemplo de Movimiento Circular Uniforme:
1. Una rueda gira a 50rpm. Calcula si velocidad angular en rad/seg, y su periodo y frecuencia.
Rpm = Revoluciones por minuto.
Necesitamos hacer factores de conversión:
Así, la velocidad angular en rad/s es: w = 1,66𝜋 rad/s
Una vez encontrada la velocidad angular encontramos el periodo con su fórmula:
Encontramos la frecuencia con la inversa del periodo:
2. La rueda de un coche de radio 50 cm gira a 400 rpm. Calcula la velocidad angular en unidades del sistema internacional y la velocidad lineal.
Primero ponemos la velocidad angular en unidades del sistema internacional:
Con la fórmula que relaciona las dos velocidades encontramos la velocidad lineal:
Pero primero tenemos que calcular el radio en unidades del SI:
r = 50 cm >> r = 0,5m
1.2) Movimiento Circular Uniformemente Acelerado (MCUA)
El Movimiento Circular Uniformemente acelerado (MCUA) es aquel que tiene aceleración constante.
Ecuación del movimiento angular:
Ecuación del movimiento lineal:
Ecuación de la velocidad angular:
Ecuación de la velocidad lineal:
Gráficos del movimiento circular uniformemente variado:
Ejemplos de ejercicios de Movimiento Circular Uniformemente Acelerado:
1. Una rueda que se encuentra en reposo adquiere una aceleración de 8 rad/s2. ¿Cuál será la velocidad angular y el ángulo que ha girado el disco 20 segundos después?
Podemos utilizar la fórmula:
2. Un coche que se encuentra inicialmente en reposo recorre un trayecto de 1000m en 70 segundos, si la rueda tiene un ángulo de 0,8m, ¿Cuál será la velocidad angular y la aceleración angular del coche?
Podemos utilizar la fórmula que relaciona la velocidad lineal y la angular para encontrar la velocidad angular:
Para poder calcular la velocidad angular, hace falta calcular primero la velocidad lineal, y para ello tendremos que calcular primero la aceleración lineal:
Ahora que sabemos la aceleración lineal, calculamos la velocidad lineal:
Ahora podemos encontrar la velocidad angular:
Ahora si podemos calcular la aceleración angular, a partir de la ecuación de la velocidad:

























No hay comentarios:
Publicar un comentario