CINEMÁTICA
La cinemática es la parte de la física, que se ocupa de
estudiar el movimiento de los objetos.
Los componentes que forman parte del movimiento son:
1. El espacio: El tramo recorrido por el móvil en el tiempo. (m)
2. Tiempo: Espacio de tiempo que tarda el móvil en recorrer el espacio. (seg.)
3. Velocidad: Relación entre el espacio recorrido y el tiempo. (m/s)
4. Aceleración: Forma en la que varía la velocidad a lo largo del tiempo. (m/s2)
1. MOVIMIENTOS RECTILÍNEOS
Son aquellos movimientos en que el móvil se desplaza en línea recta.

Tipos de movimientos rectilíneos:
1.1) Movimiento Rectilíneo Uniforme (MRU):
El movimiento rectilíneo uniforme es ese en que el móvil se desplaza en línea recta y que tiene velocidad constante. El hecho de tener velocidad constante, implica que no tiene aceleración.
Ecuación del movimiento:
Gráficas del movimiento rectilíneo uniforme:
1. Un coche, que parte desde 0 metros, se desplaza a 80km/h durante 2 horas. ¿Qué espacio habrá recorrido? Expresarlo en unidades del Sistema Internacional (SI).
Las unidades del sistema Internacional son las que están estipuladas de forma general para expresar los distintos elementos de física.
En el caso de la velocidad, en m/s. El espacio en metros y el tiempo en segundo.
Para convertir las unidades de nuestros valores, necesitamos factores de conversión:
Ahora aplicamos la fórmula para encontrar el espacio recorrido:
Respuesta: Se han recorrido 159,98 metros.
1.2) Movimiento Rectilíneo Uniformemente Acelerado (MRUA)
El movimiento rectilíneo uniformemente acelerado es ese en que el móvil se desplaza en línea recta y que tiene velocidad que aumenta de forma proporcional y una aceleración constante.
Ecuación del movimiento:
Ecuaciones de la velocidad:
Gráficos del Movimiento Rectilíneo Uniformemente Acelerado:
Ejemplo de ejercicios con MRUA:
1. Un coche va a una velocidad de 20m/s y frena con una aceleración de 2m/s2 hasta que para. ¿Cuánto tiempo tarda el coche en pararse?
Como tenemos las unidades en Sistema Internacional, solo tenemos que aplicar la fórmula para saber el tiempo que tarda en detenerse.
Utilizamos esta fórmula porque es la que incluye todos los datos que tenemos y también el tiempo, que es lo que necesitamos encontrar:
La Respuesta es 10 segundos.
**En este caso la aceleración se expresa como negativa porque el coche está frenando.
2. Un coche lleva una velocidad de 10m/s y acelera de forma que recorre 700m en 35 seg.
a) Calcula la velocidad media durante los 35seg.
Para calcular la velocidad media, necesitamos la fórmula general que al principio hemos visto:
b) Calcula la velocidad final:
Lo primero que tenemos que saber es la aceleración:
Al saber la aceleración con la siguiente fórmula encontramos la velocidad final:

Así encontramos la velocidad final, 26,41m/s.

Fórmulas que relacionan las componentes angulares y lineales:
1.3) Caída libre:
El movimiento Caída Libre es ese en que el móvil se desplaza en línea recta y vertical y que tiene velocidad que aumenta de forma proporcional y una aceleración constante.
Es decir se trata de un Movimiento Rectilíneo Uniformemente Acelerado pero en vertical.
En este caso, la aceleración será siempre la gravedad. (g=9,8m/s2)
Ecuación del movimiento:
Ecuaciones de la velocidad:

Ejemplo de ejercicios con CAÍDA LIBRE:
1. Un Cuerpo se deja caer de una altura de 2 metros. ¿Cuánto tardará en llegar al suelo, y a qué velocidad lo hará?
Para saber cuánto tardará el objeto en llegar al suelo, tenemos que utilizar la ecuación del movimiento:
Ahora una vez sabemos el tiempo, podemos encontrar con la ecuación de la velocidad, la velocidad con la que llega al suelo el objeto, es decir la velocidad final:
2. MOVIMIENTOS CIRCULARES:
Son aquellos movimientos en que la trayectoria es circular.
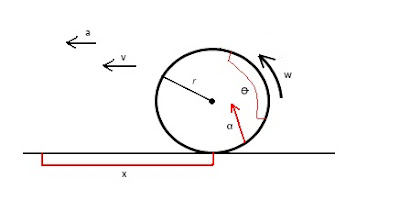
Los movimientos circulares tienen dos componentes, uno circular y otro horizontal, ya que si imaginamos una rueda, podemos contemplar como al igual que se produce un movimiento circular, este genera otro movimiento horizontal que hace que se desplace el coche.
Componente circular
|
Componente horizontal
|
Ɵ = Espacio circular recorrido
Expresamos en: rad
|
x = Espacio lineal recorrido
Expresamos en: metros
|
w = Velocidad angular
Expresamos en: rad/s
2π rad = 1 vuelta = 1 revolución
|
v= Velocidad lineal
Expresamos en: m/s
|
α = Aceleración angular
Expresamos en: rad/s2
|
a = Aceleración lineal.
Expresamos en: m/s2
|
r = Radio
|
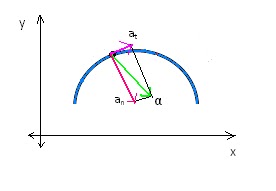
La aceleración angular tiene dos componentes:
Los dos componentes de la aceleración son perpendiculares, y así tenemos la aceleración tangencial (at) y la aceleración normal (an).
La aceleración tangencial es la que se encarga de la variación de la velocidad angular, por tanto, en movimientos uniformes, no encontraremos aceleración tangencial nunca.
Aun así la fórmula de la aceleración tangencial es:
La aceleración normal, dirigida al interior del objeto circular, se encarga de que el movimiento tenga trayectoria circular, por lo que esta aceleración estará siempre presente en un movimiento circular.
La fórmula de la aceleración normal es:
EL PERIODO Y LA FRECUENCIA:
1. Periodo: Tiempo que se tarda en dar una vuelta completa.
2. Frecuencia: Cantidad de vueltas que se dan en 1 segundo. Se mide en Hertz (Hz).
Tipos de movimientos circulares:
2.1) Movimiento Circular Uniforme (MCU):
El movimiento circular uniforme (MCU) es aquel que tiene una trayectoria circular, y que tiene velocidad angular (w) constante. Esto quiere decir que la aceleración angular es nula.
Ecuación del movimiento:
Ecuación del movimiento lineal:
Fórmula que relaciona la velocidad angular y lineal:
Gráfica del movimiento circular uniforme:
Ejemplo de Movimiento Circular Uniforme:
1. Una rueda gira a 50rpm. Calcula si velocidad angular en rad/seg, y su periodo y frecuencia.
Rpm = Revoluciones por minuto.
Necesitamos hacer factores de conversión:
Así, la velocidad angular en rad/s es: w = 1,66𝜋 rad/s
Una vez encontrada la velocidad angular encontramos el periodo con su fórmula:
Encontramos la frecuencia con la inversa del periodo:
2. La rueda de un coche de radio 50 cm gira a 400 rpm. Calcula la velocidad angular en unidades del sistema internacional y la velocidad lineal.
Primero ponemos la velocidad angular en unidades del sistema internacional:
Con la fórmula que relaciona las dos velocidades encontramos la velocidad lineal:
Pero primero tenemos que calcular el radio en unidades del SI:
r = 50 cm >> r = 0,5m
2.2) Movimiento Circular Uniformemente Acelerado (MCUA)
El Movimiento Circular Uniformemente acelerado (MCUA) es aquel que tiene aceleración constante.
Ecuación del movimiento angular:
Ecuación del movimiento lineal:
Ecuación de la velocidad angular:
Ecuación de la velocidad lineal:
Gráficos del movimiento circular uniformemente variado:
Ejemplos de ejercicios de Movimiento Circular Uniformemente Acelerado:
1. Una rueda que se encuentra en reposo adquiere una aceleración de 8 rad/s2. ¿Cuál será la velocidad angular y el ángulo que ha girado el disco 20 segundos después?
Podemos utilizar la fórmula:
2. Un coche que se encuentra inicialmente en reposo recorre un trayecto de 1000m en 70 segundos, si la rueda tiene un ángulo de 0,8m, ¿Cuál será la velocidad angular y la aceleración angular del coche?
Podemos utilizar la fórmula que relaciona la velocidad lineal y la angular para encontrar la velocidad angular:
Para poder calcular la velocidad angular, hace falta calcular primero la velocidad lineal, y para ello tendremos que calcular primero la aceleración lineal:
Ahora que sabemos la aceleración lineal, calculamos la velocidad lineal:
Ahora podemos encontrar la velocidad angular:
Ahora si podemos calcular la aceleración angular, a partir de la ecuación de la velocidad:
3. MOVIMIENTO PARABÓLICO:
El movimiento parabólico es aquel cuya trayectoria describe una parábola. Normalmente hace referencia al movimiento que genera un proyectil.
Puede ser analizado como la composición de dos movimientos: El movimiento rectilíneo uniforme (horizontal) y el movimiento rectilíneo uniformemente acelerado en vertical (o caída libre).
Esto implica que hace falta que imaginemos, que el objeto que sigue una trayectoria parabólica, lo hace, porque por un lado sigue un MRUA vertical que es el que le hace subir y bajar por el eje y (o vertical) y por otro lado sigue un movimiento MRU horizontal (o en el eje de las x) que es el que hace que avance en el plano horizontal, y no solo que suba y baje.
Gráfica del movimiento parabólico:
Tendremos que tener en cuenta que este movimiento tendrá una parte correspondiente al eje de las x y otra correspondiente al eje de las y, por lo que se tratará de un movimiento vectorial.
Fórmulas:
Tenemos que saber que: i y j son los vectores unitarios del plano. No pertenecen a ningún número, tan solo sirven para hacer referencia de a que eje pertenece cada parte. La parte que está acompañada de i pertenece al eje de las x, y la parte acompañada de j se refiere a la parte que pertenece al eje y.
Para determinar la velocidad podemos efectuar la fórmula siguiente:
** Teniendo en cuenta que la velocidad tiene componente vx y vy
Si queremos determinar la ecuación de la posición:
Podemos descomponer las fórmulas en eje x y eje y, así:
Para la velocidad:
1. Eje horizontal:
2. Eje vertical:
Para la posición:
1. Eje horizontal:
2. Eje vertical:
Para la aceleración:
1. Eje horizontal:
2. Eje vertical:
Ejemplos de problemas de movimiento parabólico:
1. Se arroja un proyectil des del suelo con un ángulo de 60º y una velocidad de 30m/s. ¿A qué altura máxima llegará la pelota y cuantos metros recorrerá?
Para saber a qué altura llegará tenemos que tener en cuenta sólo el eje de las y. Por tanto tomemos solo de referencia la parte vertical del movimiento:
Para la posición:
1. Eje horizontal:
2. Eje vertical:
|
Como en este momento tenemos como incógnita, además de la altura (y) el tiempo, tendremos que hallar primero el tiempo.
En el momento de altura máxima, lo que sucede es que el proyectil comienza a bajar, y esto significa que la vy en ese punto es 0.
Por tanto podemos obtener la t con la ecuación de la velocidad del eje y.
Para la velocidad:
1. Eje horizontal:
2. Eje vertical:
|
Ahora sabemos que la pelota llega a la altura máxima cuando el tiempo es 2,65seg. Así podemos resolver la ecuación del movimiento y, por tanto seguimos con la ecuación del movimiento del eje y:
Ahora tenemos que encontrar el punto en el que el proyectil vuelve al suelo. Con esto nos referimos a que distancia en el eje de las x se ha recorrido, por tanto, tendremos que hallar la ecuación del movimiento del eje x.
Para la posición:
1. Eje horizontal:
2. Eje vertical:
|
En este caso volvemos a tener como incógnita el tiempo, pero si reflexionamos, veremos que el momento en que el proyectil vuelve al suelo es cuando y=0, cuando ya no hay altura, así podemos encontrar el tiempo si en la ecuación de la posición del eje vertical igualamos y a 0, así:
Obtenemos una ecuación de segundo grado, que solucionamos con la fórmula de la ecuación de segundo grado:
Solución 1:
|
Solución 2:
Esta opción no puede ser porque el tiempo no puede ser 0, por lo que la opción correcta será la de la solución 1.
|
Una vez hallado el tiempo, ahora sustituyendo con la ecuación de la posición del eje x, encontramos el alcance del proyectil, es decir, la posición del suelo en que cae el proyectil:














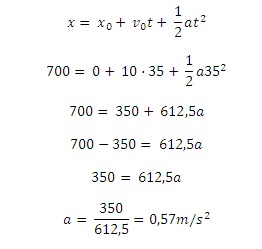















































No hay comentarios:
Publicar un comentario