OPERACIONES BÁSICAS
3. Multiplicación:
Multiplicar es igual que sumar varias veces el mismo número.
Por ejemplo:
2 x 3 = 6 y es igual que sumar 2 tres veces (2 + 2 + 2 = 6).
5 x 5 = 25 es igual que sumar 5 veces 5 (5 + 5 + 5 + 5 + 5 =
25).
Para multiplicar, lo hacemos de la siguiente manera:
Los términos de la multiplicación tienen los nombres
siguientes:
El proceso para multiplicar números más largos por una sola
cifra es el siguiente:
Empezamos a multiplicar
por la parte izquierda, y el resultado de 4
x 6 = 24.
En el resultado solo
podemos dejar una de las cifras y siempre dejaremos la de las unidades, así la
otra pasa sumando a la multiplicación de las decenas:
Ahora multiplicamos las
decenas, y después sumamos lo que llevamos de las unidades:
4 x 4 = 16 + 2 = 18
Igual que
anteriormente, dejamos las unidades y subimos al siguiente termino el resto
para sumarlo:
Finalmente
multiplicamos el último término y obtenemos el resultado (2 x 4 + 1 = 9):
Cuando multiplicamos un número por otro de más de una cifra
lo hacemos de la siguiente forma, respetando en todo caso, además, las normas
anteriores.
Por ejemplo: 234 x 21
En primer lugar multiplicamos
por el primer término que es el 1:
Ahora antes de
multiplicar por el segundo término (que colocaremos debajo del primero)
colocamos un 0 debajo de las unidades:
Multiplicamos por el
segundo término pero empezamos a colocar los números a partir de las decenas:
Para obtener el
resultado final, lo que debemos hacer es sumar lo obtenido de las
multiplicaciones:
Siempre que el número por el que multiplicamos tenga más de
una cifra seguiremos este proceso, y dejaremos siempre un 0. En el segundo
término en las unidades, pero en el siguiente en las decenas y así
sucesivamente, en función de cuantos sean los términos del número por el que
multiplicamos.
PROPIEDADES DE LA MULTIPLICACIÓN:
1. Propiedad Conmutativa: Al multiplicar no importa el orden
en que lo hagamos.
Por ejemplo:
5 x 2 = 10 y 2 x 5 = 10
2. Propiedad Asociativa: Si multiplicamos 3 o más números da
igual en el orden en que lo hagamos.
Por ejemplo:
(5 x 2) x 3 = 10 x 3
= 30 y 5 x (2 x 3) = 5 x 6 = 30
3. Propiedad Distributiva: Para multiplicar una suma,
podemos hacerlo de dos maneras. Por ejemplo:
(5 + 2) x 3 = 7 x 3 =
21 o (5 + 2) x 3 = 5 x 3 + 2 x 3 =
15 + 6 = 21
En el segundo caso estaremos aplicando la propiedad
distributiva.
4. División:
Dividir es calcular cuantas veces un número incluye a otro.
Es el proceso contrario a multiplicar.
Por ejemplo: 4 : 2 =
2
Veamos como dividimos:
Las partes que forman parte de la división son las
siguientes:
Como hacemos para dividir. Por ejemplo, para dividir:
Seleccionamos el primer
número del Dividendo, si este es más grande que el divisor empezamos a dividir,
si no lo es, debemos seleccionar el segundo término. En este caso deberemos
seleccionar los dos primeros.
Lo que hacemos a continuación
es encontrar un número que multiplicado por el divisor sea igual al número
seleccionado o menor. En este caso, necesitamos un número que multiplicado por
2 sea 11 o menor. Si reflexionamos, sabremos que 2 x 5 = 10
Colocamos el resultado
de esa multiplicación debajo del número seleccionado y restamos:
Seguidamente colocamos
el siguiente número del dividendo en lo que nos ha sobrado, así:
Ahora debemos
encontrar un número que multiplicado por 2 de 16 o menor parecido. Así, sabemos
que 2 x 8 = 16. Una vez obtenido el resultado restamos. Como ya no hay más
números en el dividendo, habremos terminado la división:
Existen diferentes tipos de división en función del resto:
- Si el
resto es igual a 0: La división es exacta. Todo el dividendo se ha podido
distribuir.
- Si el resto es distinto a 0: La
división no es exacta. Hay una parte del número que no se ha podido distribuir.
PROPIEDADES DE LA DIVISIÓN:
1. Propiedad Conmutativa: La división no cumple esta
propiedad.
Por ejemplo:
6 : 3 ≠ 3 : 6
2. Propiedad Asociativa: Se pueden descomponer factores
dividiendo para dividir obteniendo el mismo resultado. Por ejemplo:
1000 : 50 = 20 es
igual que 1000 : 50 = 1000 : 10 : 5 =
100 : 5 = 20
3. Propiedad distributiva: Se puede descomponer una suma o
resta al dividendo y después dividir por separado cada parte.
Por ejemplo:
(24 + 30 + 18) : 2 =
72 : 2 = 36
Pero también:
(24 + 30 + 18) : 2 =
24 : 2 + 30 : 2 + 18 : 2 = 12 + 15 + 9 = 36







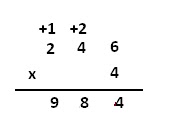












No hay comentarios:
Publicar un comentario