ESTÁTICA:
La estática, es el estudio de los objetos cuando no se
encuentran en movimiento, es decir, cuando están en equilibrio.
Este tipo de ejercicios suelen tener que ver con deportes como
la escalada, o con objetos en suspensión.
Es importante destacar, que cuando un objeto se encuentra en
equilibrio, es decir, sin movimiento, la fórmula general de la dinámica es la
siguiente:
EJEMPLO:
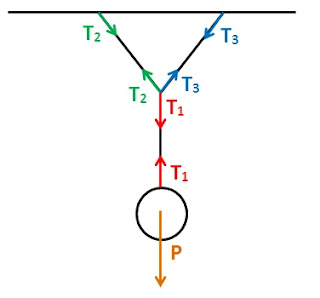
Un objeto de 2,5 Kg de masa, se encuentra suspendido en un
sistema como el siguiente, donde hay con el techo un ángulo de 45º con cada una
de las cuerdas:
Indica el valor de las tensiones que actúan en el sistema para
que el objeto se encuentre en equilibrio.
En primer lugar haremos
un esquema con las fuerzas que actúan en este sistema:
La Tensión es una
fuerza que se da cuando el objeto se encuentra sujeto por cuerdas. Es aquella
fuerza que genera la fuerza en contra del objeto. Debemos dibujarla siempre en
los dos lados de la cuerda, y saber que será la misma en un extremo y el otro
de la cuerda.
Como este sistema tiene
dos partes, debemos en primer lugar dividir el sistema en dos para encontrar
las tensiones.
En primer lugar nos
fijamos en la parte de la bola y la primera cuerda:
Si analizamos el
sistema vemos que, para que el objeto se encuentre en equilibrio, el valor de
la tensión 1 tiene que ser igual al peso del objeto, de lo contrario, el
sistema se partiría, y la bola no podría sostenerse en la cuerda. Así buscamos
el valor del peso:
El valor del peso es
24,5 N, entonces, el valor de T1 también es 24,5 N.
Una vez hemos
solucionado esta parte del sistema, nos dirigimos a solucionar la otra parte
del sistema:
En este caso, deberemos
descomponer las Tensiones 2 y 3 ya que no se haya en el mismo eje de
coordenadas que el resto de fuerzas del sistema:
En esta parte del
problema, deberemos siempre separar las fuerzas que actúan en el eje x de las
que actúan en el eje y.
Veamos que componentes actúan
en el eje x:
Esto es:
Ahora veamos que
componentes actúan en el eje y:
Esto es:
Como vemos, hemos
generado dos ecuaciones con dos incógnitas, por tanto, para solucionar esto,
debemos generar un sistema de ecuaciones:
Ahora solucionamos el
sistema con cualquiera de los métodos para resolver sistemas de ecuaciones. Yo
lo haré a través del método de Sustitución.
Ahora sabemos que T2
= T3, por lo tanto, que las dos tensiones en este caso son
iguales. Esto sucede porque el ángulo es el mismo y porque además el seno y el
coseno de 45º es el mismo.
Sustituimos en la otra
ecuación, para obtener T3:
Como hemos obtenido que
T3 y T2 son iguales, el valor de T2 también
será 17,5 N.














No hay comentarios:
Publicar un comentario