PLANOS INCLINADOS:
Cuando el objeto se encuentra en un plano inclinado en lugar de
en una superficie horizontal, es necesario descomponer fuerzas. Las fuerzas que
debemos descomponer son todas aquellas que se encuentren fuera de los ejes del
plano inclinado. Veamos:
Dibujemos las fuerzas
que actúan en este sistema. En primer lugar debemos dibujar el peso, que
siempre es perpendicular a la tierra:
En segundo lugar
dibujamos la fuerza normal, que siempre es una fuerza que ejerce el suelo, por
lo que la dibujamos así:
Para poder trabajar con
estas fuerzas debemos descomponer en un eje de coordenadas colocado a favor de
la superficie inclinada donde trabajamos:
Las fuerzas que no se
encuentren paralelas a los ejes, deberán ser descompuestas. Entonces, en este
caso, debemos descomponer el peso:
Una vez descompuestas
las fuerzas, debemos saber, que para poder solucionar los problemas necesitamos
conocer trigonometría. En este caso vemos que:
EJEMPLO:
Un objeto se desplaza por una superficie inclinada hacia abajo
sin que se aplique ninguna fuerza externa. Si la fuerza de rozamiento tiene un
coeficiente de μ = 0,2, el plano
inclinado un ángulo de 30º y el objeto una masa de 25 kg, ¿Qué aceleración
llevará el objeto?
En primer lugar debemos
hacer un esquema de las fuerzas y descomponer las que sea necesarias para poder
solucionar el problema.
Si nos fijamos, veremos
que la componente del peso del eje y, y la fuerza normal se contrarrestan. No
pasa como en el plano inclinado, donde la normal es igual al peso simplemente.
Esto quiere decir que Py
= N. Así solo actúan en el movimiento las fuerzas que tienen componente x.
Estas fuerzas serán Px, que es la que promueve el movimiento, y la fuerza de
rozamiento, que se opone al movimiento. Así debemos encontrar en primer lugar
el valor de FF:
Sabemos que:
Y en este caso, la
fuerza normal es igual a Py, por tanto:
Sabemos que Py = P · sinα, entonces:
El peso es P = m · g, entonces:
Substituimos para
encontrar la fuerza de rozamiento:
Ahora debemos encontrar
el Peso de la componente x, que será Px
= P · cosα, entonces:
Sabemos que el peso es P = m · g, entonces:
Substituimos y
encontramos la fuerza Px:
Aplicamos la fórmula
general de la dinámica:
En este caso:
Ambas fuerzas se restan porque tienen
sentidos contrarios.
Sustituyendo por los
valores encontraremos el valor de la aceleración:








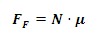










No hay comentarios:
Publicar un comentario