POSICIONES
RELATIVAS DE DOS RECTAS:
Puntos:
Un Punto sirve para indicar una posición en un plano. Los puntos no tienen dimensiones y se nombran con letras mayúsculas.
En un eje de coordenadas, los puntos se definen como (x, y),
es decir que tienen una posición en el eje x y una en el eje y, y ahí donde
confluyen esos dos puntos, es donde se encuentra ubicado dicho punto en el
mapa.
Veamos por ejemplo, para ubicar el punto A = (2, -4) en el eje de
coordenadas:
El primer
término siempre corresponde al eje de las x, en este caso, indicamos el punto
2:
A
continuación indicamos el punto de las y, que en este caso es el -4:
A
continuación trazamos dos líneas rectas hasta que confluyan los dos puntos:
Este punto
donde confluyen las dos rectas, es el que pertenece al punto (2, -4):
Una recta, es el conjunto de todos los puntos del plano
alineados donde se encuentra la línea. Además las rectas se alinean a partir de
un punto y con una dirección que es un vector. Todas las rectas podemos
definirlas numéricamente a partir de distintas ecuaciones.
Rectas:
Mediante dos puntos se determina una recta. Las rectas tienen sólo una dimensión, que es la longitud. Designamos una recta a partir de los dos puntos o con una letra minúscula.
Cuando dos rectas se cortan determinan un punto, por ejemplo en el ejemplo, las dos rectas determinan el punto E:
Según la posición que ocupan dos rectas, estas pueden ser:
a) Paralelas: Si mantienen una equidistancia entre ellas. Son rectas que nunca se tocan en ningún punto.
b) Secantes: Dos rectas son secantes si se cortan en algún punto.
Cuando las dos rectas se cortan en algún punto formando un ángulo de 90º las llamamos perpendiculares.
c) Coincidentes: Dos rectas son coincidentes cuando ocupan el mismo lugar del espacio, es decir, cuando comparten todos los puntos.
Ecuaciones de la recta:
1. Ecuación
vectorial de la recta:
Los vectores v y u pertenecen al eje de coordenadas, v pertenece al eje y,
y u al eje x, a partir de estos vectores se determina un punto X y un vector
que tiene como origen el punto P.
Como vemos
en el dibujo anterior, la recta la podemos definir tan solo con el vector v,
que indica la dirección de la recta y lo llamaremos vector director, y el punto
X y P. Entonces la recta está definida por PX.
La ecuación
vectorial vendrá determinada por el punto de la recta (X) y el vector
multiplicado por una constante.
Entonces:
Así que:
EJEMPLOS:
1. Calcula La
ecuación vectorial de la recta que pasa por el punto A (-2,4) y tiene un vector director v (2, 2):
2. Calcula la ecuación
vectorial de la recta que pasa por los puntos C(1, -1) y D(2, -4).
En este caso no tenemos
vector director, por lo que lo tendremos que calcular. El vector director será
el formado por los puntos CD:
Ahora ya tenemos el
vector director y por tanto podemos trabajar con uno de los puntos y este
vector:
2. Ecuaciones
paramétricas de la recta:
A partir de la ecuación vectorial obtendremos las ecuaciones
paramétricas de la recta.
EJEMPLOS:
1. Calcula las ecuaciones
paramétricas de la recta que pasa por el punto A (-2,4) y tiene un vector director v (2, 2):
Entonces:
2. Calcula las ecuaciones
paramétricas de una recta que pasa por los puntos C(1, -1) y D(2, -4).
En primer lugar debemos
calcular el vector director, que pasara por los mismos puntos que la recta, por
lo que lo calculamos así:
Ahora si calculamos las
ecuaciones paramétricas de la recta:
Entonces:
3. Ecuación continua
de la recta:
Para formar esta ecuación despejaremos la constante k de las
ecuaciones paramétricas.
EJEMPLOS:
1. Calcula la ecuación
continua de la recta que pasa por el punto A (-2,4) y tiene un vector director v (2, 2):
Entonces:
2. Calcula la ecuación
continua de una recta que pasa por los puntos C(1, -1) y D(2, -4).
En primer lugar debemos
calcular el vector director, que pasara por los mismos puntos que la recta, por
lo que lo calculamos así:
Ahora calculamos la
ecuación continua de la recta:
Entonces:
4. Ecuación punto
pendiente de la recta:
A partir de la ecuación continua de la recta, generaremos la
ecuación punto pendiente:
EJEMPLO:
1. Calcula la ecuación
continua de la recta que pasa por el punto A (-2,4) y tiene un vector director v (2, 2):
Calculamos la
pendiente:
Entonces calculamos la
ecuación punto pendiente de la recta:
Entonces:
2. Calcula la ecuación
continua de una recta que pasa por los puntos C(1, -1) y D(2, -4).
En primer lugar debemos
calcular el vector director, que pasara por los mismos puntos que la recta, por
lo que lo calculamos así:
A continuación
calculamos la inclinación a partir del vector:
Ahora calculamos la
ecuación punto pendiente de la recta:
Entonces:
3. Calcula la ecuación
punto pendiente de la recta que pasa por el punto A (2, 3) y que tiene una inclinación
de 45º.
Para saber el valor de
la inclinación cuando nos dan la inclinación en grados tendremos que hacer la
tangente:
Ahora que sabemos que
la inclinación es 1, m = 1, entonces calculamos la ecuación de la recta:
Entonces:
5. Ecuación
implícita de la recta:
La ecuación implícita de la recta, también la llamamos ecuación
general de la recta. A partir de la ecuación continua de la recta, generaremos
la implícita:
Con esta ecuación, las componentes del vector director serán:
Además la pendiente de la recta será:
EJEMPLO:
1. Calcula la ecuación continua de una recta
que pasa por los puntos C(1, -1) y D(2, -4).
En primer lugar debemos
calcular el vector director, que pasara por los mismos puntos que la recta, por
lo que lo calculamos así:
A continuación hacemos
la ecuación continua de la recta:
A partir de ésta
generamos la implícita de la recta:
2. Calcula la ecuación
general de la recta que pasa por el punto (2, 3) y tiene una pendiente de m =
2:
Como nos dan la
pendiente, llegaremos a la ecuación implícita a través de la ecuación punto
pendiente:
Ahora igualamos a cero
esta para obtener la ecuación implícita:
6. Ecuación explícita
de la recta:
Al despejar y en la ecuación general de la recta, obtenemos la
ecuación explícita de la recta:
EJEMPLOS:
1. Calcula la ecuación
explícita de la recta que pasa por el punto (2, 3) y tiene una pendiente de m =
2:
En primer lugar
calculamos la ecuación punto pendiente de la recta:
Ahora transformamos
esta ecuación en la explícita:





















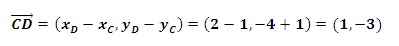






























No hay comentarios:
Publicar un comentario