MATEMÁTICAS: ECUACIONES - La ecuación de cuarto grado y las ecuaciones bicuadradas

ECUACIONES DE CUARTO GRADO:

Las ecuaciones de cuarto grado son aquellas cuya mayor potencia de x es 4. Por ejemplo:

Para resolver estas ecuaciones lo hacemos como cualquier ecuación que tenga más que grado dos. Es decir, a partir del método Ruffini.

Veamos cómo solucionarlo con un ejemplo:

PASO 1: Colocamos la ecuación por orden de grado, empezando por el grado cuatro al 0, y dejando a un lado todos los términos del igual. En nuestro caso, ya tenemos colocada la ecuación de esta forma.

PASO 2: Hacemos el método Ruffini dos veces y una ecuación de segundo grado para encontrar los cuatro resultados, o también podemos realizar 4 veces el método Ruffini y encontrar los cuatro resultados posibles de x. Lo vemos:

[Si quieres saber más del método Ruffini entra aquí]

Así obtenemos dos soluciones, ya que las cuatro se repiten. Las soluciones serán -1 y 2.

LA ECUACIÓN BICUADRADA:

Las ecuaciones bicuadradas son un tipo de ecuación de cuarto grado que tiene una forma concreta. La estructura de las ecuaciones bicuadradas es la siguiente:

Veamos cómo resolverlo:

PASO 1: Para empezar, tendremos que colocar la ecuación en la forma de arriba. Como en nuestro ejemplo ya lo está pasaremos al siguiente paso. Si no lo está deberemos realizar los pasos adecuados, cambiando términos de lado del igual o realizando las operaciones necesarias, como hemos visto en otros casos.

PASO 2: Ahora convertiremos la ecuación bicuadrada en una de segundo grado cambiando la incógnita de x a z, pero dejando el resto de la ecuación igual. Sabiendo que z = x²:

PASO 3: Realizamos la ecuación de segundo grado para encontrar los dos valores de z:

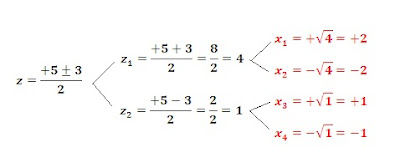
PASO 4: Ahora tenemos ya los dos valores de z, pero nosotros lo que queremos encontrar es x. Para encontrar x tendremos que hacer la raíz cuadrada de los resultados de z, encontrando la raíz positiva y negativa. Lo vemos:

Así encontraremos las 4 soluciones de una ecuación bicuadrada.